1. Normal Strains
As a result of bending, somewhere between the top and bottom of the beam is a surface in which the longitudinal fibres do not change in length. This surface is called the neutral surface of the beam and its intersection with any cross-sectional plane is called the neutral axis of the cross-section.
All the longitudinal fibres other than those in the neutral surface either lengthen or shorten, thereby creating longitudinal strains ![]() .
.
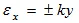
Where k = curvature = 1/R
This equation shows longitudinal strains are proportional to the curvature and that they vary linearly with the distance y from the neutral surface. This equation is derived from the geometry of the deformed beam and is independent of the properties of the material. The equation is valid irrespective of the stress-strain diagram of the material.
2. Transverse Strain
The axial strains ![]() are accompanied by lateral or transverse strains due to the effect of Poisson’s ratio. Positive strains are accompanied by negative transverse strains
are accompanied by lateral or transverse strains due to the effect of Poisson’s ratio. Positive strains are accompanied by negative transverse strains ![]() .
.
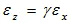
Where ![]() is the Poisson’s Ratio.
is the Poisson’s Ratio.
As a result of these strains, the shape of the cross-section change. For example, let us study the case of a beam of rectangular cross-section subjected to pure bending so as to induce tension at the top and compression at the bottom.
The sides of the rectangular cross-section become inclined to each other. The top surface becomes saddle shaped. If the longitudinal curvature in the xy plane is considered positive, then the transverse curvature in the yz plane is negative. All planes of the beam that were initially parallel to neutral surface develop antiplastic curvature.
Applicability of Flexure Formula
The normal stresses determined from flexure formula concern pure bending, which means no shear forces act on the cross-section. In case of non-uniform bending the presence of shear forces produces warping or put of place distortion of the cross-section, thus, a section that is plane before bending is no longer plane after bending.
Warping due to shear greatly complicates the behaviour of the beam, but more elaborate analysis shows that the normal stresses calculated from the flexure formula are not significantly altered by the presence of the shear stresses and the associated warping. Thus use of the theory of pure bending for calculating normal stresses in cases of non-uniform bending is considered justified.
