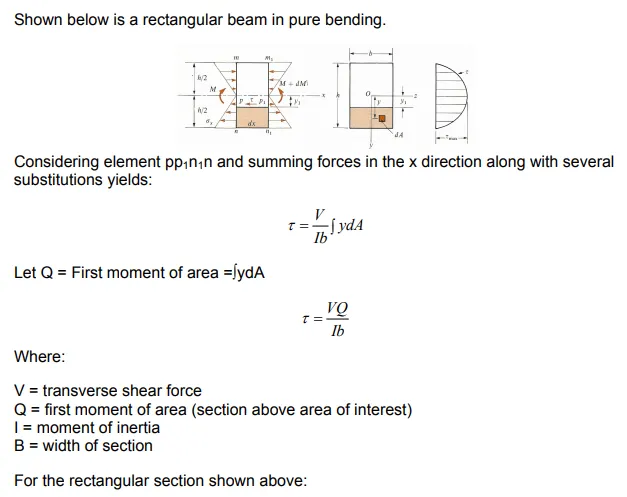
Shear Stress in Beams: When a beam is subjected to nonuniform bending, both bending moments, M, and shear forces, V, act on the cross section. The normal stresses, σx, associated with the bending moments are obtained from the flexure formula. We will now consider the distribution of shear stresses, τ, associated with the shear force, V. Let us begin by examining a beam of rectangular cross section. We can reasonably assume that the shear stresses τ act parallel to the shear force V. Let us also assume that the distribution of shear stresses is uniform across the width of the beam.

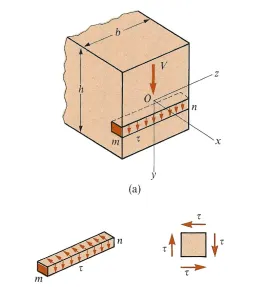
Shear stresses on one side of an element are accompanied by shear stresses of equal magnitude acting on perpendicular faces of an element. Thus, there will be horizontal shear stresses between horizontal layers (fibers) of the beam, as well as, transverse shear stresses on the vertical cross section. At any point within the beam these complementary shear stresses are equal in magnitude. The existence of horizontal shear stresses in a beam can be demonstrated as follows.

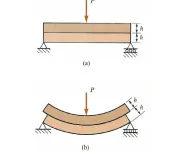
A single bar of depth 2h is much stiffer that two separate bars each of depth h.