Architectural structures are normally stationary. Most clients, building officials and designers prefer that their structures remain static rather than move dynamically. There are specific loading conditions which are dynamic loads, but in each and every case a return to a stable and static state is desireable. Such a condition is known as equilibrium.
Various states of static equilibrium are experinced throughout one’s life. Think of the “teeter-totter” at a playground or of a game of “tug-of-war.” In the first case, two or more individuals sit upon a board which has been fixed to a fulcrum which allows rotation. If each of the individuals on the teeter totter weight exaclty the same amount and sit at exactly the same distance from the fulcrum the teeter-totter will not move. A state of equilibrium has been achieved. The two will remain at rest until an action takes them out of equilibrium.

Such an action could be the addition of another person to the system or it could be that one of the original two would change their position slightly. In either case, the teeter-totter would most likely swing to one side and rest upon the ground. A new state of equilibrium would have been found.
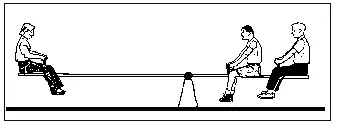
In this case, another child climbed on in front of the one already sitting on the right. In order to put the system back into equilibrium the child on the left had to move backwards along the board until she was far away. The moment the two children created around the fulcrum almost doubled when the second child climbed on. The girl knew that the only way that she could increase the magnitude of the moment she created would be to increase the moment arm (lever arm). Thus, she moved back until she was about twice as far from the fulcrum. At that point the system would be put back into equilibrium.
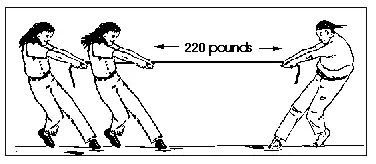
Another example of a state of equilibrium is the game of “tug-of-war.” A rope is pulled taut between two teams; each hopes to pull with at least a force that equals the force imposed by the opposite team. Assume that each team in the figure is pulling with a force of 220 pounds. The system is in equilibrium long as each team maintains the tension force of 220 pounds. If a device would be inserted between the two teams along the rope to measure the magnitude of the tension force within the rope, it would read 220 pounds at each and every point along the rope. This would be true at ANY point along the rope. Equilibrium would be lost if either any of the competition would suddenly release the rope.

A structure is in equilibrium when all forces or moments acting upon it are balanced. This means that each and every force acting upon a body, or part of the body, is resisted by either another equal and opposite force or set of forces whose net result is zero. Sir Issac Newton addressed this issue when he noted that a body at rest will remain at rest until acted upon by an external force. Every structure that can be seen to remain standing on a daily basis is in equilibrium; it is at rest and each of its members, combination of its members or any part of a member that is supporting a load, are also at rest. There is a net result of zero in all directions for all of the applied loads and reactions.
This is a node from the Olympic Stadium in Munich designed by Frei Otto. The massive cast iron shape is held in place by the tensile forces imparted by each of the cables which are attached to it.
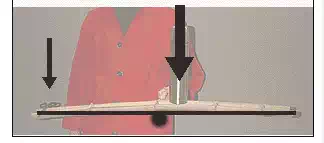
In this illustration a piece of split bamboo is held so that it is in equilibrium. The point of the fulcrum is very close to the center of the length of the piece. This illustrates a system in equilibrium under it’s own weight. Two items are then added to the bamboo; a coffee thermos and a pair of scissors.

The split bamboo beam remains in a state of equilibrium. The scissors rests at a great distance from the fulcrum in order to balance the heavier weight of the thermos on the opposite side. All of the forces and moments must be balanced so that the system is in a stable equilibrium. 
There are two types of equilibrium; External and Internal. External equilibrium encompasses the loads upon, and reactions of, a structural system as a whole. Internal equilibrium describes the various forces the are acting within every member of the system. There are conditions of equilibrium that must be satisfied for both types. These are:
Sum of All Vertical Forces (Fy) = 0
Sum of All Horizontal Forces (Fx) = 0
Sum of All Moments (Mz) = 0
(Sum of All Forces (Fz) = 0)
(Sum of All Moments (My) = 0)
(Sum of All Moments (Mx) = 0)
These six equations are all that can be used to determine every one of the forces that are acting with a structure. They are few, but very powerful. The first three are the most common equations and will be utilized in all of the problems associated with this course. The other three are only necessary when considering three-dimensional force systems.

