The client in the initial design phase develops a program, or list of requirements. The goal of the designers is to select a system that meets these requirements. Before the designers do this, however, it is advisable for them to question whether the requirements represent the client’s actual needs. Can the criteria and standards affecting the design be made less stringent? After the program has been revised to answer these questions, the designers select a system. Next, it is advisable for the designers to question whether the system provides the best value at the lowest cost. Value engineering is a useful procedure for answering this question and selecting a better alternative if the answer indicates this is desirable. Value engineering is the application of the scientific method to the study of values of systems. The major objective of value engineering in building design and construction is reduction of initial and life-cycle costs. Thus, value engineering has one of the objectives of systems design, in which the overall goal is production of an optimum building, and should be incorporated in the systems design procedure.

The scientific method, which is incorporated in the definitions of value engineering and systems design, consists of the following steps:

1. Collection of data and observations of natural phenomena

2. Formulation of a hypothesis capable of predicting future observations

3. Testing of the hypothesis to verify the accuracy of its predictions and abandonment or improvement of the hypothesis if it is inaccurate

Those who conduct or administer value studies are often called value engineers, or value analysts. They generally are organized into an interdisciplinary team for value studies for a specific project. Sometimes, however, an individual, such as an experienced contractor, performs value engineering services for the client for a fee or a percentage of savings achieved by the services.

Value Analysis.

Value is a measure of benefits anticipated from a system or from the contribution of a component to system performance. This measure must be capable of serving as a guide in a choice between alternatives in evaluations of system performance. Because generally in comparisons of systems only relative values need be considered, value takes into account both advantages and disadvantages, the former being considered positive and the latter negative. It is therefore possible in comparisons of systems that the value of a component of a system may be negative and subtracts of systems from the overall performance of the system.

System evaluations would be relatively easy if a monetary value could always be placed on performance. Then, benefits and costs could be compared directly.

Value, however, often must be based on a subjective decision of the client. For example, how much extra is an owner willing to pay for beauty, prestige, or better community relations? Will the owner accept gloom, glare, draftiness, or noise for a savings in cost? Consequently, other values than monetary must be considered in value analysis. Such considerations require determination of the relative importance of the client’s requirements and weighting of values accordingly.

Value analysis is the part of the value-engineering procedure devoted to investigation of the relation between costs and values of components and systems and alternatives to these. The objective is to provide a rational guide for selection of the lowest-cost system that meets the client’s actual needs.

Measurement Scales.

For the purposes of value analysis, it is essential that characteristics of a component or system on which a value is to be placed be distinguishable. An analyst should be able to assign different numbers, not necessarily monetary, to values that are different. These numbers may be ordinates of any one of the following four measurement scales: ratio, interval, ordinal, nominal.

Ratio Scale.

This scale has the property that, if any characteristic of a system is assigned a value number k, any characteristic that is n times as large must be assigned a value number nk. Absence of the characteristic is assigned the value zero. This type of scale is commonly used in engineering, especially in cost comparisons. For example, if a value of $10,000 is assigned to system A and of $5000 to system B, then A is said to cost twice as much as B.

Interval Scale.

This scale has the property that equal intervals between assigned values represent equal differences in the characteristic being measured. The scale zero is assigned arbitrarily. The Celsius scale of temperature measurements is a good example of an interval scale. Zero is arbitrarily established as the temperature at which water freezes; the zero value does not indicate absence of heat. The boiling point of water is arbitrarily assigned the value of 100. The scale between 0 and 100 is then divided into 100 equal intervals called degrees (C). Despite the arbitrariness of the selection of the zero point, the scale is useful in heat measurement. For example, changing the temperature of an objective from 40C to 60C, an increase of 20C, requires twice as much heat as changing the temperature from 45C to 55C, an increase of 10C.

Ordinal Scale.

This scale has the property that the magnitude of a value number assigned to a characteristic indicates whether a system has more, or less, of the characteristic than another system has or is the same with respect to that characteristic. For example, in a comparison of the privacy afforded by different types of partitions, each may be assigned a number that ranks it in accordance with the degree of privacy that it provides. Partitions with better privacy are given larger numbers. Ordinal scales are commonly used when values must be based on subjective judgments of nonquantifiable differences between systems.

Nominal Scale.

This scale has the property that the value numbers assigned to a characteristic of systems being compared merely indicate whether the systems differ in this characteristic. But no value can be assigned to the difference. This type of scale is often used to indicate the presence or absence of a characteristic or component. For example, the absence of a means of access to equipment for maintenance may be represented by zero or a blank space, whereas the presence of such access may be denoted by 1 or X.

Weighting.

In practice, construction cost usually is only one factor, perhaps the only one with a monetary value, of several factors that must be evaluated in a comparison of systems. In some cases, some of the other characteristics of the system may be more important to the owner than cost. Under such circumstances, the comparison may be made by use of an ordinal scale for ranking each characteristic and then weighting the rankings in accordance with the importance of the characteristic to the owner.

As an example of the use of this procedure, calculations for comparison of two partitions are shown in Table 1.1. Alternative 1 is an all-metal partition and alternative 2 is made of glass and metal.

In Table 1.1, characteristics of concern in the comparison are listed in the first column. The numbers in the second column indicate the relative importance of each characteristic to the owner: 1 denotes lowest priority and 10 highest priority. These are the weights. In addition, each of the partitions is ranked on an ordinal scale, with 10 as the highest value, in accordance with the degree to which it possesses each characteristic. These rankings are listed as relative values in Table 1.1. For construction cost, for instance, the metal partition is assigned a relative value of 10 and the glass-metal partition a value of 8, because the metal partition costs a little less than the other one. In contrast, the glass-metal partition is given a relative value of 8 for visibility, because the upper portion is transparent, whereas the metal partition has a value of zero, because it is opaque.

To complete the comparison, the weight of each characteristic is multiplied by the relative value of the characteristic for each partition and entered in Table 1.1 as a weighted value. For construction cost, for example, the weighted values are 8  10 80 for the metal partition and 8  8 64 for the glass-metal partition. The weighted values for each partition are then added, yielding 360 for alternative 1 and 397 for alternative 2. While this indicates that the glass-metal partition is better, it may not be the best for the money. To determine whether it is, the weighted value for each partition is divided by its cost, yielding 0.0300 for the metal partition.

TABLE 1.1 Comparison of Alternative Partitions*

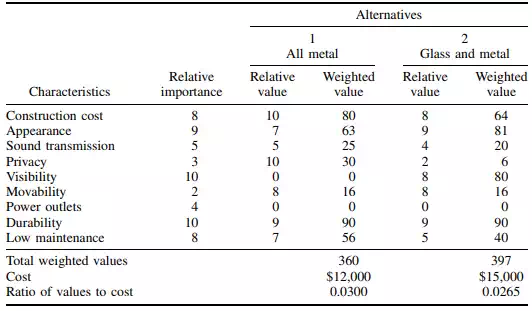
and 0.0265 for the other. Thus, the metal partition appears to offer more value for the money and would be recommended.

Economic Comparisons.

In a choice between alternative systems, only the differences between system values are significant and need to be compared.

Suppose, for example, the economic effect of adding 1 in of thermal insulation to a building is to be investigated. In a comparison, it is not necessary to compute the total cost of the building with and without the insulation. Generally, the value analyst need only subtract the added cost of 1 in of insulation from the decrease in HVAC cost to obtain the net saving or cost increase resulting from addition of insulation. A net saving would encourage addition of insulation. Thus, a decision can be reached without the complex computation of total building cost.

In evaluating systems, value engineers must take into account not only initial and life-cycle costs but also the return the client wishes to make on the investment in the building. Generally, a client would like not only to maximize profit, the difference between revenue from use of the building and total costs, but also to ensure that the rate of return, the ratio of profit to investment, is larger than all of the following:

·         Rate of return expected from the type of business

·         Interest rate for borrowed money

·         Rate for government bonds or notes

·         Rate for highly rated corporate bonds

The client is concerned with interest rates because all costs represent money that must be borrowed or that could otherwise be invested at a current interest rate. The client also has to be concerned with time, measured from the date at which an investment is made, because interest cost increases with time. Therefore, in economic comparisons of systems, interest rates and time must be taken into account. (Effects of monetary inflation can be taken into account in much the same way as interest.)

An economic comparison usually requires evaluation of initial capital investments, salvage values after several years, annual disbursements and annual revenues. Because each element in such a comparison may have associated with it an expected useful life different from that of the other elements, the different types of costs and revenues must be made commensurable by reduction to a common basis. This is commonly done by either:

1. Converting all costs and revenues to equivalent uniform annual costs and income

2. Converting all costs and revenues to present worth of all costs and revenues at time zero.

Present worth is the money that, invested at time zero, would yield at later times required costs and revenues at a specified interest rate. In economic comparisons, the conversions should be based on a rate of return on investment that is attractive to the client. It should not be less than the interest rates the client would have to pay if the amount of the investment had to be borrowed. For this reason, the desired rate of return is called interest rate in conversions. Calculations also should be based on actual or reasonable estimates of time periods. Salvage values, for instance, should be taken as the expected return on sale or trade-in of an item after a specific number of years that it has been in service. Interest may be considered compounded annually.

Future Value.

Based on the preceding assumptions, a sum invested at time zero increases in time to

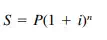                                                                  (1.1)

where

S = future amount of money, equivalent to P, at the end of n periods of time with interest

i = i interest rate

n = number of interest periods, years

P = sum of money invested at time zero present worth of S

Present Worth.

Solution of Eq. (1.1) for P yields the present worth of a sum of money S at a future date:

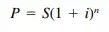                                                                (1.2)

The present worth of payments R made annually for n years is

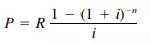                                                      (1.3)

The present worth of the payments R continued indefinitely can be obtained from Eq. (1.3) by making n infinitely large:

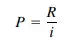                                                                              (1.4)

Capital Recovery.

A capital investment P at time zero can be recovered in n years by making annual payments of

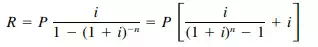                         (1.5)

When an item has salvage value V after n years, capital recovery R can be computed from Eq. (1.5) by subtraction of the present worth of the salvage value from the capital investment P.

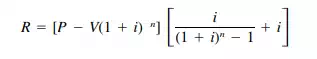                        (1.6)

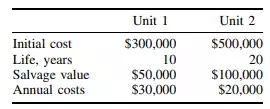
Example. To illustrate the use of these formulas, an economic comparison is made in the following for two air-conditioning units being considered for an office building. Costs are estimated as follows:

                                                    

Cost of operation, maintenance, repairs, property taxes, and insurance are included in the annual costs. The present-worth method is used for the comparison, with interest rate i= 8%.

Conversion of all costs and revenues to present worth must be based on a common service life, although the two units have different service lives, 10 and 20 years, respectively. For the purpose of the conversion, it may be assumed that replacement assets will repeat the investment and annual costs predicted for the initial asset. (Future values, however, should be corrected for monetary inflation.) In some cases, it is convenient to select for the common service life the least common multiple of the lives of the units being compared. In other cases, it may be more convenient to assume that the investment and annual costs continue indefinitely. The present worth of such annual costs is called capitalized cost.

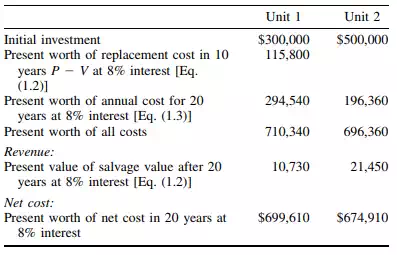
For this example, a common service life of 20 years, the least common multiple of 10 and 20, is selected. Hence, it is assumed that unit 1 will be replaced at the end of the tenth period at a cost of $300,000 less the salvage value. Similarly, the replacement unit will be assumed to have the same salvage value after 20 years.

The calculations in Table 1.2 indicate that the present worth of the net cost of unit 2 is less than that for unit 1. If total cost during the twenty-year period were the sole consideration, purchase of unit 2 would be recommended.

ASTM has developed several standard procedures for making economic studies of buildings and building systems, in addition to ASTM E917 for measuring lifecycle costs, mentioned previously. For example, ASTM E964 is titled Practice for Measuring Benefit-to-Cost and Savings-to-Investment Ratios for Buildings and Building Systems. Other standards available present methods for measuring internal rate of return, net benefits, and payback. ASTM also has developed computer programs for these calculations.

Value Analysis Procedure.

In building design, value analysis generally starts with a building system or subsystem proposed by the architect and consultants. The client or the client’s representative appoints an interdisciplinary team to study the system or subsystem and either recommend its use or propose a more economical alternative. The team coordinator sets goals and priorities for the study and may appoint task groups to study parts of the building in accordance with the priorities. The value analysts should follow a systematic, scientific procedure for accomplishing

 

 

TABLE 1.2 Example Comparison of Two Air-Conditioning Units

                      

all the necessary tasks that comprise a value analysis. The procedure should provide an expedient format for recording the study as it progresses, assure that consideration has been given to all information, some of which may have been overlooked in development of the proposed system, and logically resolve the analysis into components that can be planned, scheduled, budgeted, and appraised.

The greatest cost reduction can be achieved by analysis of every component of a building. This, however, is not practical, because of the short time usually available for the study and because the cost of the study increases with time. Hence, it is advisable that the study concentrate on those building systems (or subsystems) whose cost is a relatively large percentage of the total building (or system) cost, because those components have possibilities for substantial cost reduction.

During the initial phase of value analysis, the analysts should obtain a complete understanding of the building and its major systems by rigorously reviewing the program, proposed design and all other pertinent information. They should also define the functions, or purposes, of each building component to be studied and estimate the cost of accomplishing the functions.

Value engineering should start during the conceptual phase of design. Then, it has the greatest impact on cost control and no cost is involved in making design changes. During later design phases, design changes involve some cost, especially when substitution of major subsystems is involved, but the cost is nowhere near as great as when changes are made during construction. Such changes should be avoided if possible. Value engineering, however, should be applied to the project specifications and construction contract. Correction of unnecessary and overconservative specifications and contract provisions offers considerable potential for cost reduction.