Design of sawn timber columns and compressive members

Design requirements.

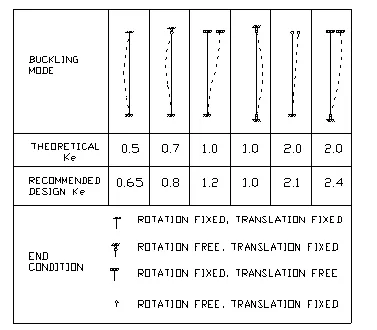
1. The slenderness ratio L_e/d for solid column shall not exceed 50 for service load and shall not exceed 75 for construction. L_e=K_e´L is effective length of column, Ke is slenderness ratio, L is unsupported length of column.  For rectangular section, L_e/d shall be evaluated in both directions.
2. Maximum compressive stress, fc must not exceed allowable stress parallel to grain, F’_c = F_c*C_D*C_M*C_t*C_F*C_p

Where

F_c is allowable bending stress in NDS supplement.

C_D is load duration factor, (see beam design)

C_M is wet service factor, (use when moisture of timber is higher than 19%)

C_t is temperature factor, (when timber is used in temperature higher than 150°F)

C_F is size factor, (apply only to visually graded sawn lumber members, and to round timber bending members, not apply simultaneously with Cv for glued laminated timber)

C_p is column stability factor (see below)

Slenderness ratio, K_e

Column stability factor C_p

Design procedure for timber column and compressive members

1. Select timber species and section.
2. Calculate slenderness ratio for both axes, L_ex/d_x, L_ey/d_y, where L_ex=L_x*K_ex, L_ey=L_y*K_ey.  K_ex and K_ey, are slenderness ratios in x and y direction. L_x and L_y are unsupported length in x and y direction.
3. Determine maximum compressive stress, f”_c=P/A. P is column axial load.  A is cross section area.
4. Determine allowable compressive stress, F_c*

F_c* = F_c´C_D´C_M´C_t´C_F

Where

F_c is allowable bending stress in NDS supplement.

C_D is duration factor,

C_M is wet service factor, (use when moisture of timber is higher than 19%)

C_t is temperature factor, (when timber is used in temperature higher than 150°F)

C_F is size factor, (apply only to visually graded sawn lumber members, and to round timber bending members, not apply simultaneously with C_v for glued laminated timber)

5. Calculate elastic modulus

E’=E´C_M´C_t

            Where E is modulus of elasticity in NDS supplement

6. Calculate F_cE= K_cE*E’/(L_e/d)²
7. Calculate C_p
8. Calculate allowable compressive stress,

F”_c = F_c*´C_p

Example 4: Design of sawn timber column:

Design data:

Floor area supported by column:  A = 80 ft²

Unsupported length of column, L = 10 ft

Hinge support at top and bottom of column

Design load:

Floor live load: W_L = 30 psf

Floor dead load: W_D = 10 psf

Superimposed dead load: W_SD = 5 psf

Timber: Southern pine, moisture less than 19%, used in normal room temperature.

Solution:

1. Select southern pine, 4″x4″ stud grade, d = 3.5 in

Actual cross section: A_c = 12.25 in2.

Allowable compressive stress parallel to grain: F_c = 975 psi

2. Calculate slenderness ratio: K_e = 1, L_e =K_e´L = 10 ft, L_e/d = 34 < 50

3. Calculate compressive stress with load duration factor

Load duration factor for dead load: C_D = 0.9

Load duration factors for live load: C_D = 1.0 (Use 1 per NDS)

Calculate Design load: P = [W_D + W_SD+ W_L]´A = 3600 lb

Column compressive stress, f_c=P/A_c = 293.8 psi

4. Calculate allowable stress without C_p.

C_M=1, C_t=1, C_f=1

F_c* = F_c´C_M´C_t´C_F = 975 psi

5. Calculate elasticity modulus

E’=E´CM´Ct = 1.4´10⁶ psi

6. Calculate F_cE

K_cE=0.3

F_cE= K_cE*E’/(L_e/d)²= 357.3 psi

7. Calculate C_p

c = 0.8

C_p = 0.333

8. Calculate allowable compressive stress

F”_c = F_c*´C_p = 324.8 psi               >          f_c= 293.8 psi     O.K.

Example 5: Design of timber load bearing stud wall

Design data:

Tributary width of floor supported by wall: B = 20 ft².

Unsupported height of stud wall, L = 10 ft

Hinge support at top and bottom of stud wall

Design load:

Floor live load: W_L = 30 psf

Floor dead load: W_D = 10 psf

Superimposed dead load: W_SD = 5 psf

Timber: Southern pine, moisture less than 19%, used in normal room temperature.

Solution:

1. Select southern pine, 2″x4″ stud grade at 16″ O.C. d₁ = 3.5 in, d₂ = 1.5 in, s = 16 in

Actual cross section: A_c = 5.25 in².

Allowable compressive stress parallel to grain: F_c = 975 psi

2. Calculate slenderness ratio:

K_e = 1, L_ex = K_e´L = 10 ft, L_ex/d₁=34 < 50

Provide blocking at mid-height in d₂ direction

L_ey=K_e´(L/2) = 5 ft, L_ey/d₂=40 < 50 Govern

3. Calculate compressive stress with load duration factor

Load duration factor for dead load: C_D = 0.9

Load duration factors for live load: C_D = 1.0 (Use 1 per NDS 2001)

Calculate Design load: P = [W_D + W_SD+ W_L]´B´s = 1200 lb

Column compressive stress, f_c=P/A_c = 228.5 psi

4. Calculate allowable stress without C_p

C_M=1, C_t=1, C_f=1

F_c* = F_c´C_D´C_M´C_t´C_F = 975 psi

5. Calculate elasticity modulus

E’=E´C_M´C_t = 1.4´10⁶ psi

6. Calculate F_cE

K_cE=0.3

F_cE= K_cE*E’/(L_e/d)²= 262.5 psi

7. Calculate C_p

c = 0.8

C_p = 0.252

8. Calculate allowable compressive stress

F”_c = F_c*´C_p = 246 psi                  >          f_c= 228.5 psi        O.K.